
Chiefly, it works well with common shapes like circles, squares, and cones, where it can calculate how volume, area, or other parameters change as dimensions shift. For example, if a balloon is being inflated, the calculator can find how quickly the radius changes as volume increases. Whether applied to geometrical shapes, movement scenarios, or scientific experiments, this tool assists in calculating how the rate of one variable affects another.
What is a Variance Calculator and How Does it Work?
Enter a data set for a population or sample to calculate variance using the calculator below. In this equation, σ2 refers to population variance, xi is the data set of population, μ is the mean of the population data set, and N refers to the size of the population data set. Try the sample variance calculator above to check the accuracy of steps and results.
Variance Formula
The variance for a sample is equal to the sample standard deviation squared. The sum of squares SS is equal to the sum of the squared deviations of each value from the mean. Thus, the variance for a population σ² is equal to the sum of squares ∑(xi – μ)² divided by the population size N. The formula for population variance can be used to estimate the variance of the underlying distribution from which the data arises.
How to calculate variance by hand?
Unlike population variance, when calculating the sample variance, you divide by (n – 1); in this case, the resulting statistic is unbiased. To calculate the variance from a set of values, specify whether the data is for an entire population or from a sample. Values must be numeric and may be separated by commas, spaces or new-line. The sample standard deviation is the square root of the calculated variance of a sample data set. As mentioned above, the formula to calculate population variance is slightly different from sample variance.
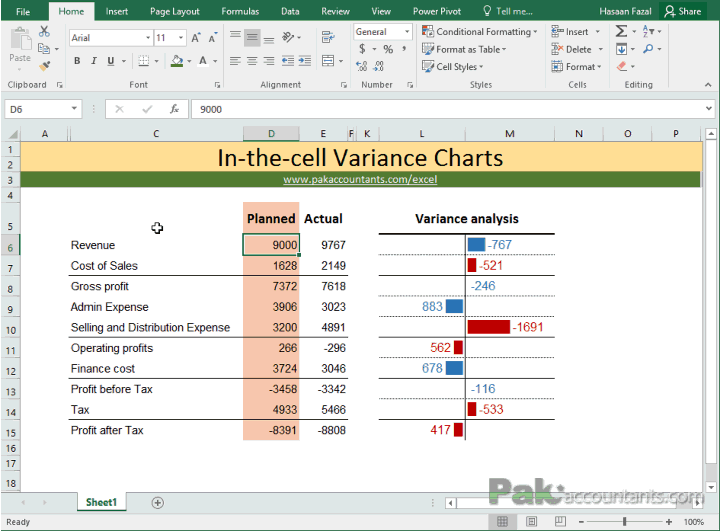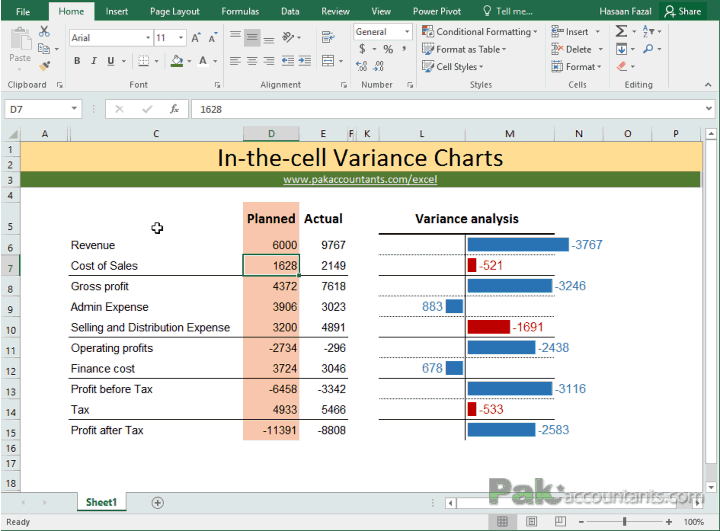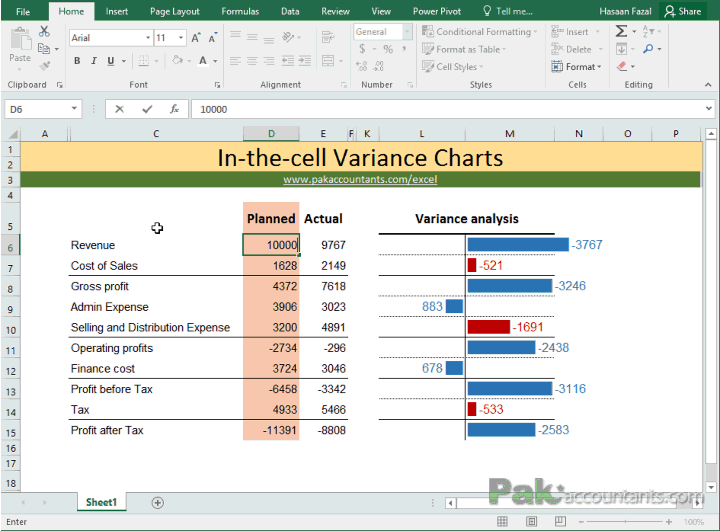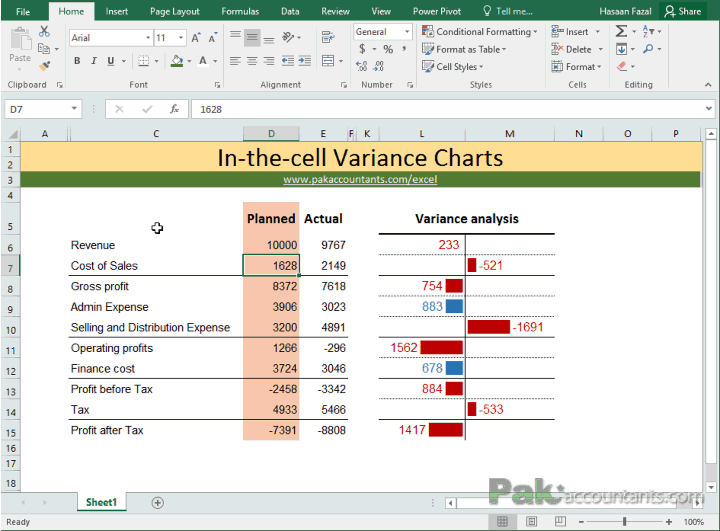
Understanding and accurately calculating variance, both for a sample and an entire population, is essential for making informed decisions based on data. This guide will delve into various aspects of variance calculation, emphasizing the role of a Variance Calculator in simplifying this process. The formula for variance of a is the sum of the squared differences between each data point and the mean, divided by the number of data values. This calculator uses the formulas below in its variance calculations. Use the following formula to calculate sample variance when dealing with sample data sets.
Population vs. sample variance formula
You can use this tool to understand and solve complex and lengthy variance problems. You can solve this problem by using the population variance calculator above or manually. This process can be facilitated using a sample variance calculator. Variance is vital in many fields, from finance to scientific research. Understanding this helps in making more informed decisions and in evaluating the reliability of data. Scientists can look for differences between test groups to determine if they are similar enough to test a hypothesis successfully.
- This guide will delve into various aspects of variance calculation, emphasizing the role of a Variance Calculator in simplifying this process.
- High variance indicates that data values have greater variability and are more widely dispersed from the mean.
- Note that the formula may be heavily biased if there are less than ten data points in a sample.
- This tool will help you better understand the concept of this metric.
- The next step is to calculate the square for each deviation from the mean found in the previous step.
Use this online variance calculator which works for both sample and population datasets using population and sample variance formula. This is the best educational calculator that tells you how to calculate the variance of given datasets in a fraction of a second. Usually, you don’t have access to the entire population’s data because it can be costly to gather all the data or may damage the sample. The sample average is a bit closer to the center of the sample than the population average. As a result, if you were to divide by n, on average, the sample average would be greater than the population variance. Dividing by (n-1) will correct the biased estimation of the variance, and partially correct the biased estimation of the variance (Bessel’s correction).
The deviation from the mean for each observation is equal to its value minus the mean x̄. The term “population” refers to the entire number of relevant observations. Analyzing Tokyo’s residents’ age, for example, would include the age of every Tokyo resident in the population.
If the variance is greater, it shows that the random variable is far from the average value. The small variance tells that the random data values are closer to the mean. While the greater variance indicates that the random data values are far from the mean. The variance calculator accepts the input as a list of numbers separated by a delimiter.
Enter any numbers (including negative numbers or decimals) and the tool will return the variance. The variance of a group or set of numbers is a number that represents the ‘spread’ of the set. Formally, this is the square of deviation in the set from the mean best barcode software for small business and the square of the standard deviation. In other words, a small variance means that the data points tend to be close to the mean and very close to each other. A high variance indicates that the data points are far away from the mean and each other.
Formally, it is the squared deviation of a variable in a set from the set’s mean and is the square of the standard deviation. To find the mean of the given data set, substitute all values in the formula and divide by the sample size n. Thus, the variance for a sample s is equal to the sum of squares ∑(xi – x̄)² divided by the sample size n minus 1. Scroll the above table for more results.Choose the population variance only if you have the data from the entire population, otherwise use the sample variance.
